calculation for the transformation in world space

Matrix is very powerful. Especially "World matrix" is very useful to "bake animation" for exporting to the other softwares. There is pretty nice tutorial "Enter the Matrix Knob" in this nukepedia.com. Well, "Camera" node, "Light" node and "Axis" node have this "World matrix" knob. And "TransfromGeo" node doesn't have it in its property.

Sometimes I want to get the values in this "World matrix" after "TransformGeo" and as they mean the final transformation, I mean it is some kinds of "the transformation in world space".

Simple example

First of all, I will show you "link" or "parent" with "matrix".

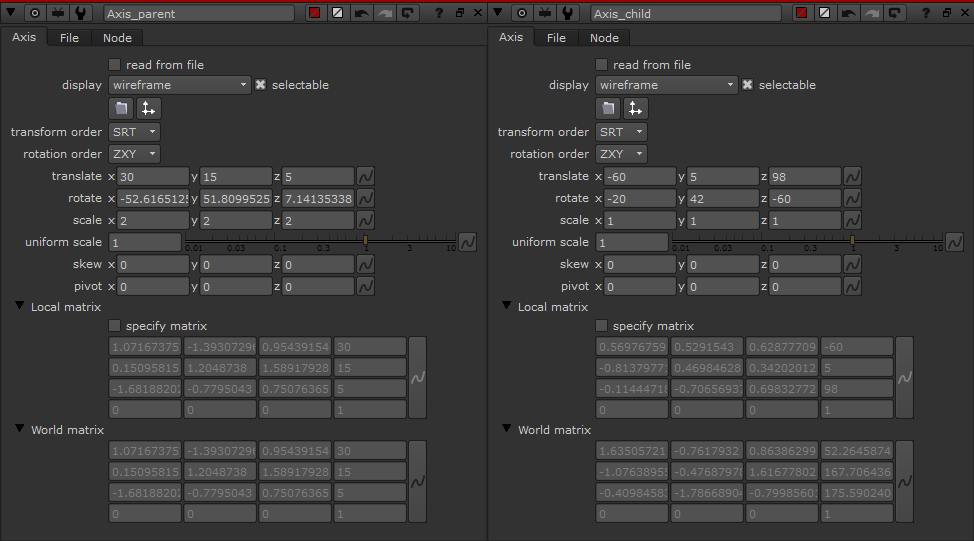
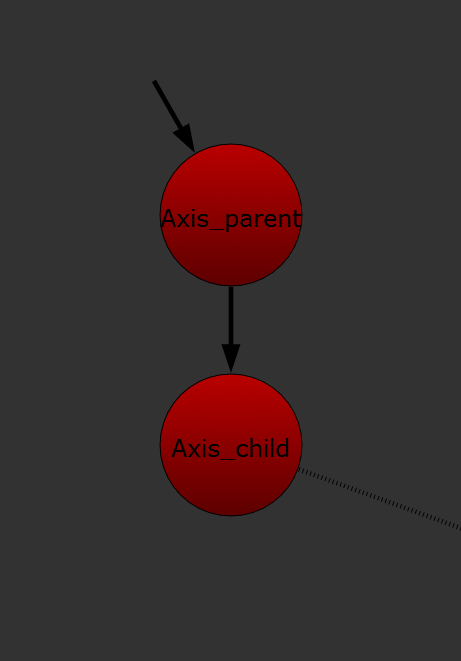
Here are two "Axis" nodes with simple connection.

"Axis" node has both "World" and "Local" matrix knob. "World matrix" means the final transformation at that node. "Local matrix" means just how much "translate","rotate" and "scale" at that node.

Let's see their "matrix"

"Local matrix" and "World matrix" have same values in "Axis_parent". And ones of "Axis_child" are two different. In this case,"Axis_parent" is a kind of "root" or "top" node, so they must be same, and "Axis_child" is affected by "Axis_world". This is why the values in "Axis_child" are different.

And Let's calculate for this "World matrix" of "Axis_child" with python. We can get it the multiple with matrix.

The multiple oreder has to be "the matrix of child * the matrix of parent".  This is very important.

So it can be written.....

World matrix of Axis_child = Local matrix of Axis_child * World matrix of Axis_parent

In python like this

1
2
3
4
5
6
7
8
9
10
11
12
13

import math

mAxisParent = nuke.math.Matrix4()
mAxisChild = nuke.math.Matrix4()

for i in range(0,16):
    mAxisParent[i] = nuke.toNode("Axis_parent")['matrix'].valueAt(nuke.frame())[i]
    mAxisChild[i] = nuke.toNode("Axis_child")['matrix'].valueAt(nuke.frame())[i]

print mAxisChild * mAxisParent

#result:
{1.63506, -0.761793, 0.863863, 52.2646, -1.07639, -0.47688, 1.61678, 167.706, -0.409846, -1.78669, -0.799856, 175.59, 0, 0, 0, 1}

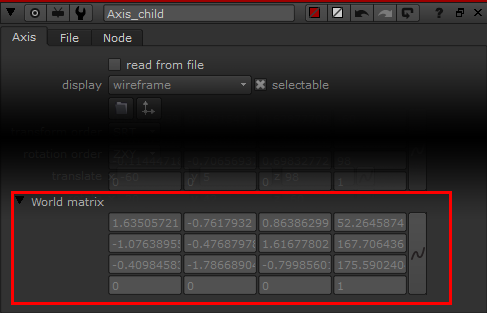
Let's compare this with "World matrix" in "Axis_local".

{1.63506, -0.761793, 0.863863, 52.2646, -1.07639, -0.47688, 1.61678, 167.706, -0.409846, -1.78669, -0.799856, 175.59, 0, 0, 0, 1}

They are same!!

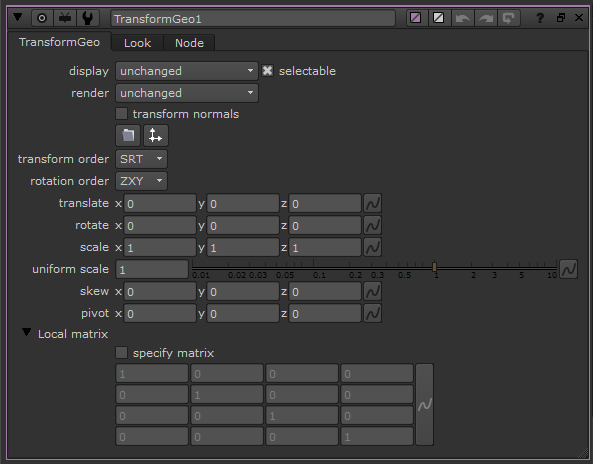
Working with "TransformGeo"

"TransformGeo" node desn't have "World matrix" knob. So we cannot get final transformation in world space so easily.

And we can make some kind of complicated combination.

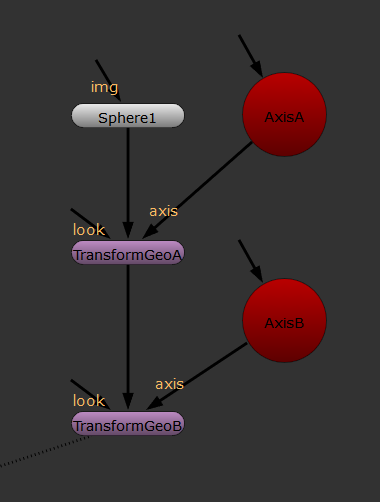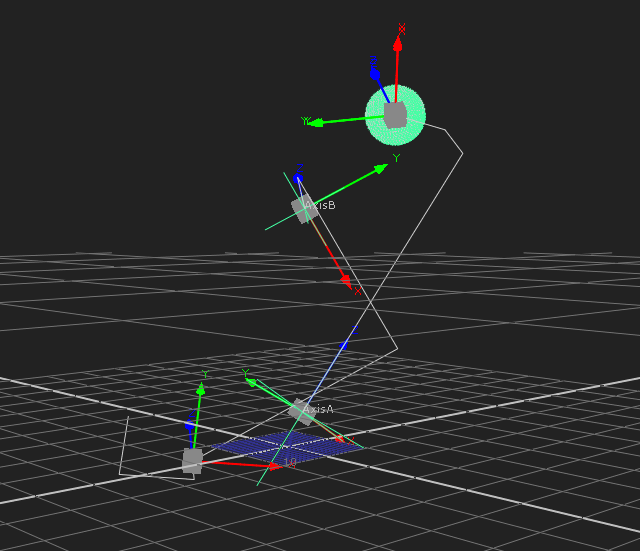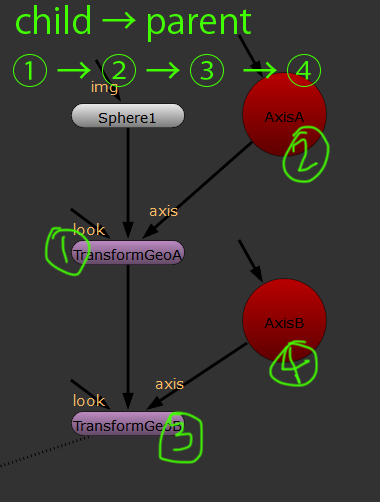
The relationship of child and parent is like this

Well, the order of the multiple is....

The transformation of "Sphere" = matrix of "TranformGeoA" * matrix of "AxisA" * matrix of "TranformGeoB" * matrix of "AxisB"

in python like this

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

import math

mAxisA = nuke.math.Matrix4()
mAxisB = nuke.math.Matrix4()
mTransformGeoA = nuke.math.Matrix4()
mTransformGeoB = nuke.math.Matrix4()

mResult = nuke.math.Matrix4()

for i in range(0,16):
    mAxisA[i] = nuke.toNode("AxisA")['matrix'].valueAt(nuke.frame())[i]
    mAxisB[i] = nuke.toNode("AxisB")['matrix'].valueAt(nuke.frame())[i]
    mTransformGeoA[i] = nuke.toNode("TransformGeoA")['matrix'].valueAt(nuke.frame())[i]
    mTransformGeoB[i] = nuke.toNode("TransformGeoB")['matrix'].valueAt(nuke.frame())[i]

mResult = mTransformGeoA * mAxisA * mTransformGeoB * mAxisB

AxisResult = nuke.createNode("Axis")
AxisResult.setName("Axis_result")

AxisResult['useMatrix'].setValue(True)

for i in range(0,16):
    AxisResult['matrix'].setValueAt(mResult[i], nuke.frame(), i)

#Result

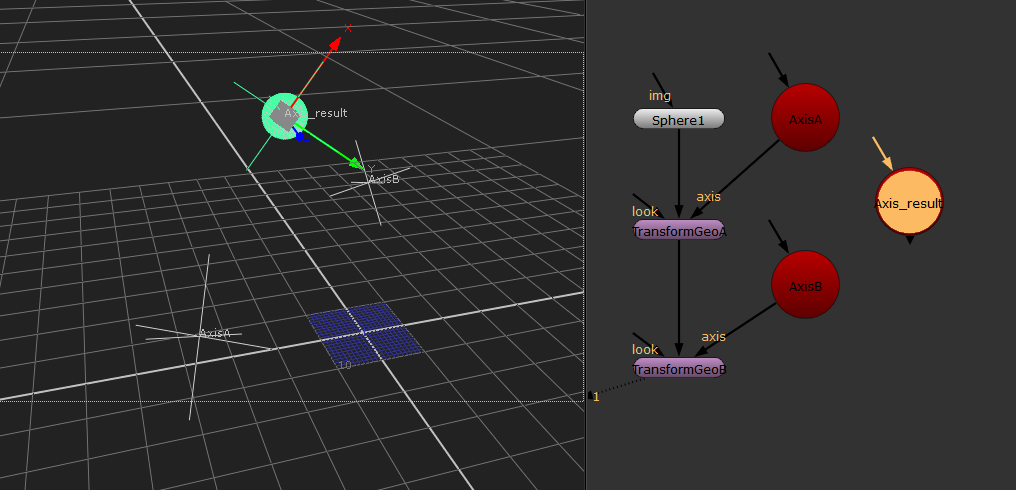
This code make "Axis" node named "Axis_result" which has the answer of this multiplication.

Once excute this code, eventually we can get "Axis_result" which has same transformation of "Sphere1"

For good measure

We can get not only matrix but just simple "translate", "rotate" and "scale" as well.

translationOnly(), rotationOnly() and scaleOnly() can provide us those values.

in python like this

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import math

mResult = nuke.math.Matrix4()

for i in range(0,16):
    mResult[i] = nuke.toNode("Axis_result")['matrix'].valueAt(nuke.frame())[i]

mResult.transpose()

mTranslate = nuke.math.Matrix4(mResult)
mTranslate.translationOnly()
mRotate = nuke.math.Matrix4(mResult)
mRotate.rotationOnly()
mScale = nuke.math.Matrix4(mResult)
mScale.scaleOnly()

translate = (mTranslate[12], mTranslate[13], mTranslate[14])
rotateRad = mRotate.rotationsZXY()
rotate = (math.degrees(rotateRad[0]), math.degrees(rotateRad[1]), math.degrees(rotateRad[2]))
scale = (mScale.xAxis().x, mScale.yAxis().y, mScale.zAxis().z)

print tanslate, rotate, scale

#result
(-12.173063278198242, 47.61678695678711, 14.971372604370117) (31.856541873883902, -121.69981885766695, 118.28480623493063) (1.4999998807907104, 1.4999998807907104, 1.4999998807907104)

Thanks,